图
柯尼斯堡七桥问题

本课程介绍的图,指的不是传统意义上的图片,而是图论中的“图”。
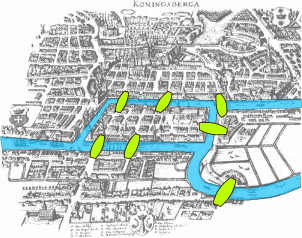
图论始于 18 世纪初期的柯尼斯堡七桥问题。
柯尼斯堡当时是普鲁士的城市,普雷格尔河穿过柯尼斯堡,不仅把柯尼斯堡分成了两部分,而且还在河中间形成了两个小岛。这就将整个城市分割成了四个区域,各区域由七座桥连接。在所有的桥都只能走一遍的前提下,如何能把这个地方所有的桥都走一遍呢?
大家可以思考一下这个问题的答案。
图论


数学家欧拉于 1735 年提出,并没有方法能圆满解决这个问题,并在第二年发表论文,证明符合条件的走法并不存在。这篇论文在圣彼得堡科学院发表,成为图论史上第一篇重要文献。
在论文中,欧拉把实际的抽象问题简化为平面上的点与边组合,将城市的四个区域抽象成点,将连接城市的七座桥抽象成连接点的边。

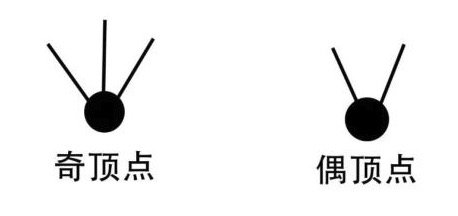
这样若从某点出发后最后再回到这点,则这一点的线数必须是偶数,这样的点称为偶顶点。相对的,连有奇数条线的点称为奇顶点。欧拉论述了,由于柯尼斯堡七桥问题中存在4个奇顶点,它无法实现符合题意的遍历。
欧拉发表的相关论文被认为是图论领域的第一篇文章,因此普遍认为欧拉是图论的创始人。
图论中的相关概念,我们将在后面的学习中提到。简单来说,图论就是研究图的学问。图是基本研究对象,用于表示实体与实体之间的关系。
图的定义

图论中的图在英文中被称为 Graph ,在中文中,强调为“拓扑图”、“网络图”等。这一名词最早由西尔维斯特在 1878 年提出。他是著名的英国数学家、牛津大学几何教授,用图来表示数学和化学分子结构之间的关系。
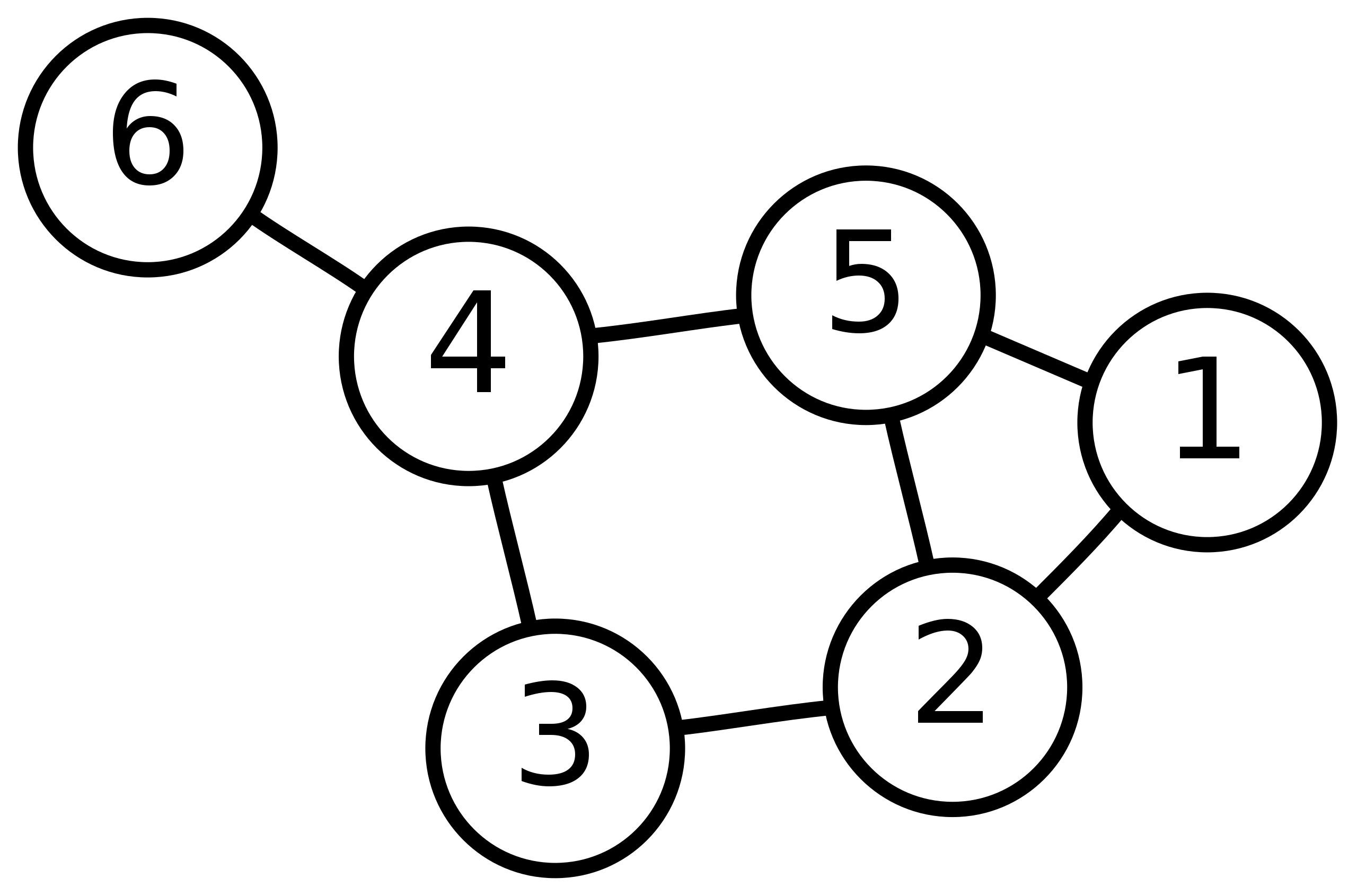
图由一些小圆点和连接这些圆点的直线或曲线组成。小圆点称为顶点或节点,直线或曲线称为边。
例如下面红色的圆圈表示一个点,蓝色的连接4、5的直线称为边。
从数学角度来说,图论是研究建模对象之间关系结构的学科。
在网络理论中,图可以用来做可视化的社会网络分析,研究社会实体之间的关系结构。

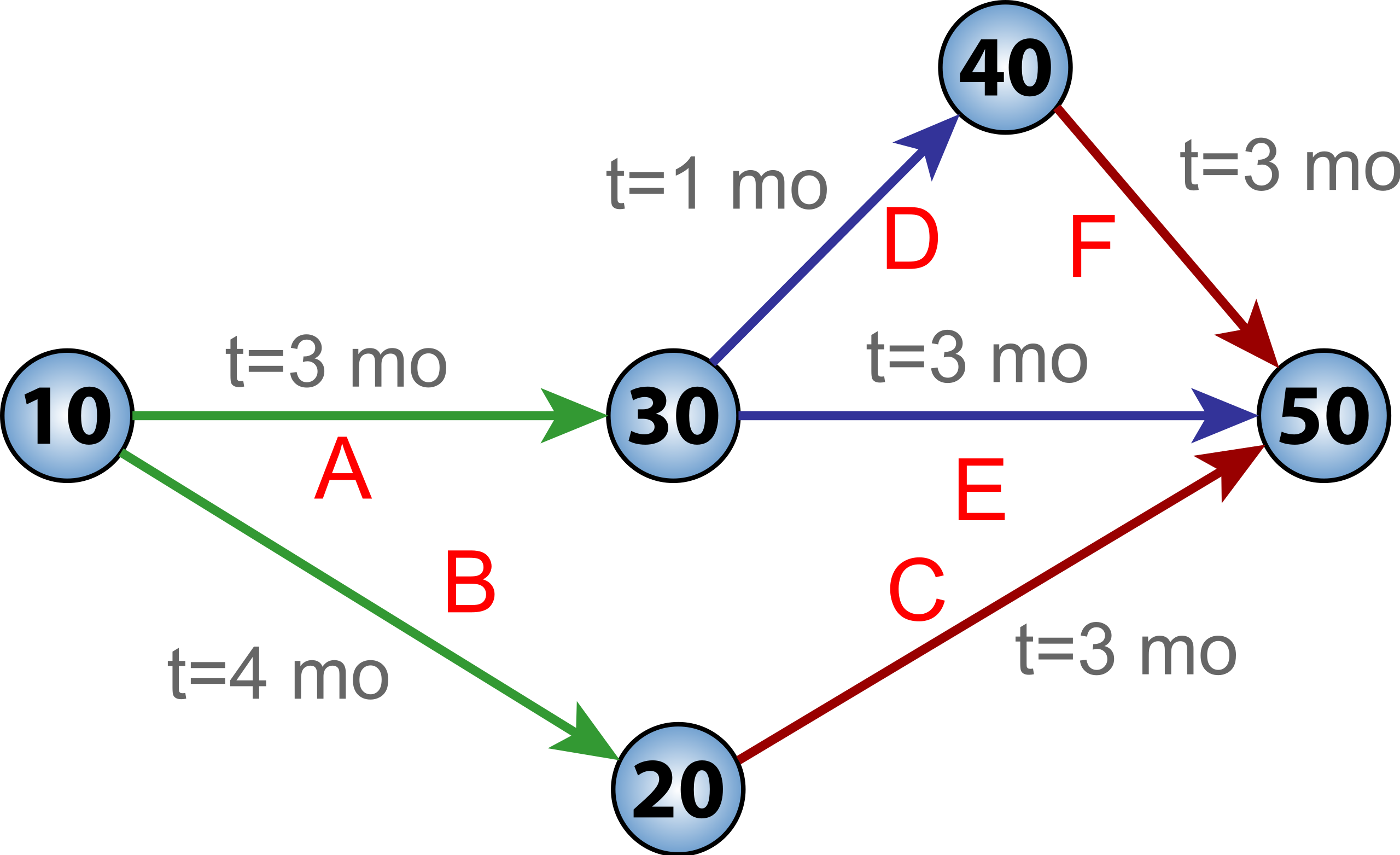
在运筹学中,以下 PERT 图可以提供一个基于图论的商业管理技术,针对不确定性较高的工作项目,用网络图规划整个项目,以排定期望的项目时程表。
在基础医学领域,图也被用来研究分子网络、疾病预测等等。
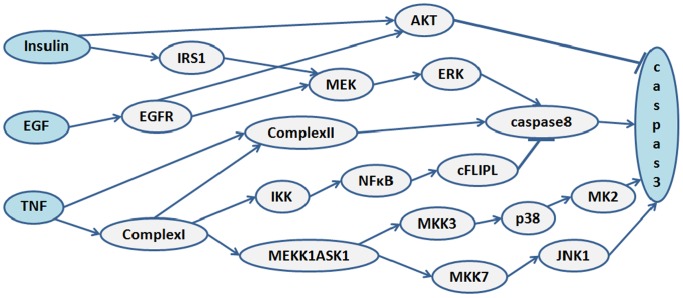
由此可见,图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程,许多实际问题可以用图来表示。因此,图论成为运筹学、控制论、信息论、网络理论、社会科学、语言学、计算机科学等众多学科强有力的数学工具。
课堂小测试
1、以下关于图的说法,错误的是?