图结构
上节课介绍了图论中图的概念,本节课将介绍图的结构,也称为图拓扑。
基本元素
图由两个基本元素构成:点和边。
点代表网络关系中的实体;边代表实体和实体之间的关系。
点
点在图数据库中也被称之为节点,可用来存储数据实体、物品、事件、地点等。
例如在转账交易中,点可以存储账户;在社媒网评中,点可以存储用户名;在历史事件中,点可以存储历史发生的事件。
下面的图片中的两点分别代表了篮球队中的球员和球队,科比·布莱恩特(Kobe Bryant)和湖人队(Lakers)。

我们可以将点存储为任意实体,但是如何体现点和点之间的联系?接下来我们看下什么是图中的边。
边
我们可以在点和点之间插入边,让点和点之间形成关系。这种关系也就被称为边。
图数据库中的关系可以用动词表示,例如,账户A转账至账户B,A和B相互关注并且A和B都关注C。

还可以用表示为附属关系。例如,张三拥有一辆汽车;乾隆是雍正的儿子等等。
点和点之间插入一条边,在上方的关系图中,在点科比·布莱恩特和点湖人队之间插入一条serve边,插入边后,即代表科比曾效力于湖人队。

点和点之间可以插入多条边,在柯尼斯堡七桥问题中,2 点之间有的是 1 条边,有的是 2 条边。
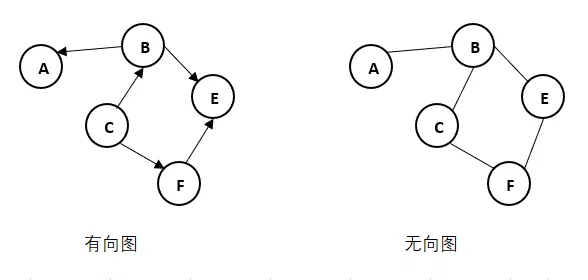
下面例子中左边图是有方向的,C指向B,B指向A,这样的图称为有向图;右边图中每条边都没有方向,则称为无向图,A和B只是连接并没有明确的方向。无向图中,两点之间的关系是双向的或者对等的。
其他元素
图除了点和边基本元素外,常见的还有以下元素:
悬挂边
悬挂边(Dangling Edge)是指一条边的起点或终点不存在于数据库中的边。关于悬挂边的详细描述,参见悬挂边。
子图
子图指节点集和边集分别是某一图的节点集的子集和边集的子集的图。
属性
点和边都可以附加属性。属性由键(key)和值(value)构成。例如,颜色:蓝色。在数据模型层面,我们把键称为"属性名称"。关于属性的更多介绍,参见课程属性图。
路径
在有向图中,有限或无限条边构成了一条路径。有向图中遍历图的路径类型分为三种:walk、trail、path。关于路径的详细描述,参见课程路径。
walk
walk 类型的路径由有限或无限的边序列构成。遍历时点和边可以重复。
trail
trail 类型的路径由有限的边序列构成。遍历时只有点可以重复,边不可以重复。
path
path 类型的路径由有限的边序列构成。遍历时点和边都不可以重复。
课堂小测试
1、点被用来存储什么?