路径
定义和分类
今天的课程介绍图论中一个重要的概念——路径。路径是指一个有限或无限的边序列,这些边连接着一系列点。路径的类型可以分为三种:walk、trail和path,在不同的路径类型之下遍历出来的图也会不一样。
为了让大家更好的理解这几个概念的不同,我们用 Dutor 和 Simon 小伙伴给大家展示。假设 Dutor 住在 A 地,而 Simon 住在 C 地,现在 Dutor 想要去 Simon 家。
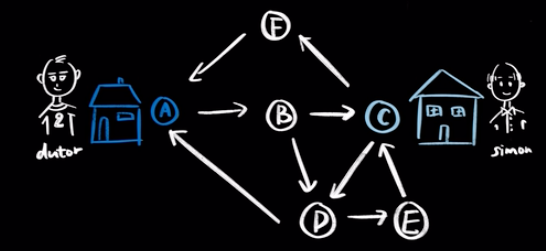
walk
如果他采用的是walk方式,从 A 点出发,他可以去到每一个地点,走每一条路,最后再到到达 Simon 家。他可以走 A→B→C 也可以走 A→B→D→E→C。甚至还可以在走到 D 点的时候,发现自己东西忘记带了回一趟家,走 A→B→D→A→B→C,经过了 A 到 B 的这条边两次。
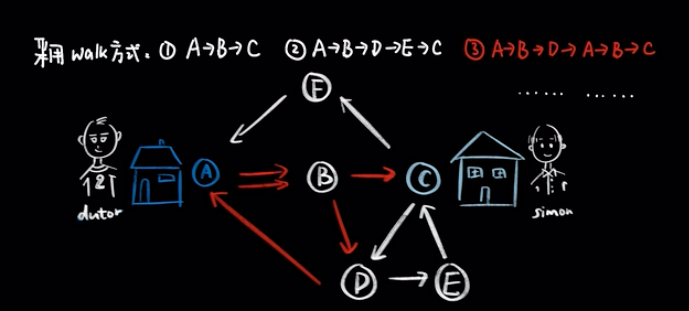
通俗的来说,walk就像是在小区跑步的你,每一条路和地点你都可以到达并且重复地走。walk类型的路径由无限或者有限的边序列构成,遍历的时候点和边都可以重复。
在 NebulaGraph 中,原生 nGQL 的 GO 语句采用的是walk类型路径。关于 GO 语句的详细介绍,期待后续课程喔。
trail
如果 Dutor 采用的是trail方式,他的可选路径就会受到很大的限制,他不能再半路掉头回去,否则他就会停在自己的家里。
因为trail类型的路径遍历时只有点可以重复,边不可以重复。从 A 出来的边只有 A→B,并且之前已经走过这条路了。他可以走 A→B→C 或者是 A→B→D→E→C 当然也可以走 A→B→C→D→E→C。
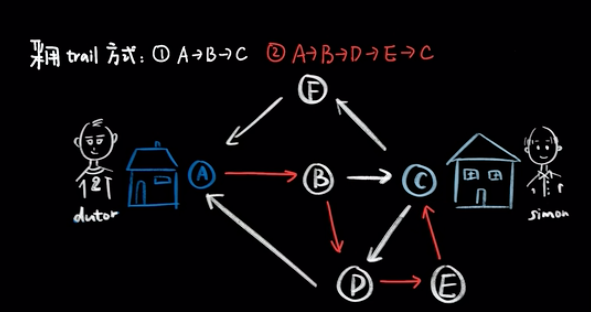
简单的来说,trail就像是只能走一次的吊桥,一旦已经走过去了,吊桥也就塌陷了。
在trail类型中,存在两种特殊的路径类型,cycle和circuit。这两个类型都是起点和终点重复,也就是说 Dutor 最后会回到自己的家。
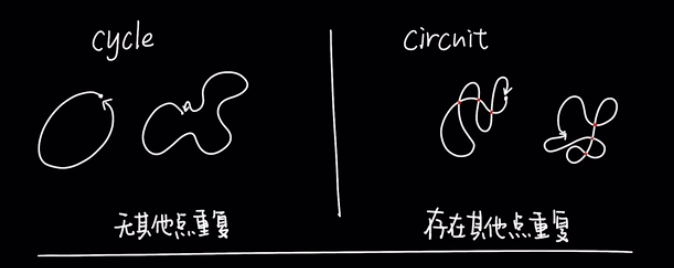
cycle只有起点和终点重复之外没有别的点重复,他可以走 A->B->C->F->A 或者是 A->B->C->D->A。circuit除了起点和终点重复之外,可能还存在其他重复点,他可以走 A->B->C->D->E->C->F->A,在这里他经过了两次 C 点。
MATCH、FINDPATH 和 GET SUBGRAPH 语句采用的是trail类型路径。关于这些语句的详细介绍,期待后续课程喔。
path
如果 Dutor 采用的是path 方式,他只有两种方式到达 Simon 的家,走 A→B→C 或者走 A→B→D→E→C。这是因为path 方式遍历时点和边都不可以重复。
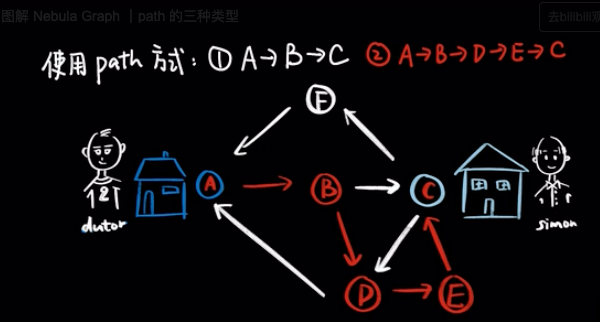
简单来说,path 就像是一条只能前进的路,一旦往前移动,身后的桥和陆地都会消失。
总结
相信到这里大家已经大概清楚这三种不同路径的概念啦。为了方便更好的区分这三种不同的概念,可以以下表格内容:
| walk | trail | path | |
|---|---|---|---|
| 路径长度 | 有限/无限 | 有限 | 有限 |
| 点是否可重复 | 是 | 是 | 否 |
| 边是否可重复 | 是 | 否 | 否 |
课堂小测试
1、遍历时点和边可以重复的路径类型是?